Publication Type:
Journal ArticleSource:
IEEE Transactions on Visualization and Computer Graphics, IEEE Computer Society, Volume 15, Issue 4, Number 4, Los Alamitos, CA, USA, p.630-641 (2009)URL:
http://doi.ieeecomputersociety.org/10.1109/TVCG.2008.201Keywords:
animation, BCC, flow visualization, optimal regular sampling, physically based modeling, vector field data, Visual simulation, volume modeling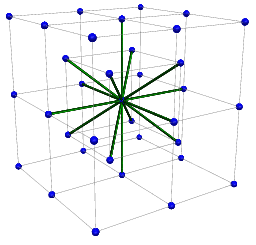
The D3bQ15 Lattice
In this paper, we extend the single relaxation time Lattice-Boltzmann Method (LBM) to the three-dimensional body-centered cubic (BCC) lattice. We show that the D3bQ15 lattice defined by a fifteen neighborhood connectivity of the BCC lattice is not only capable of more accurately discretizing the velocity space of the continuous Boltzmann equation as compared to the D3Q15 Cartesian lattice, it also achieves a comparable spatial discretization with 30% less samples. We validate the accuracy of our proposed lattice by investigating its performance on the 3D lid-driven cavity flow problem and show that the D3bQ15 lattice offers significant cost savings while maintaining a comparable accuracy. We demonstrate the efficiency of our method and the impact on graphics and visualization techniques via the application of line-integral convolution on 2D slices as well as the extraction of streamlines of the 3D flow. We further study the benefits of our proposed lattice by applying it to the problem of simulating smoke and show that the D3bQ15 lattice yields more detail and turbulence at a reduced computational cost.
